Quickly find out how loud your speakers will be based on amplifier power, speaker sensitivity, and distance from the speaker with this calculator:
Speaker SPL Calculator
I’m going to show you how this calculator works. First, we need to understand the difference between power, intensity and pressure level…
In a typical system, an amplifier will provide an electrical signal to a speaker. A portion of this electrical energy will be converted into acoustic energy by the speaker, while the rest will be converted to heat. The total acoustic energy created by the speaker is referred to as the sound power level.
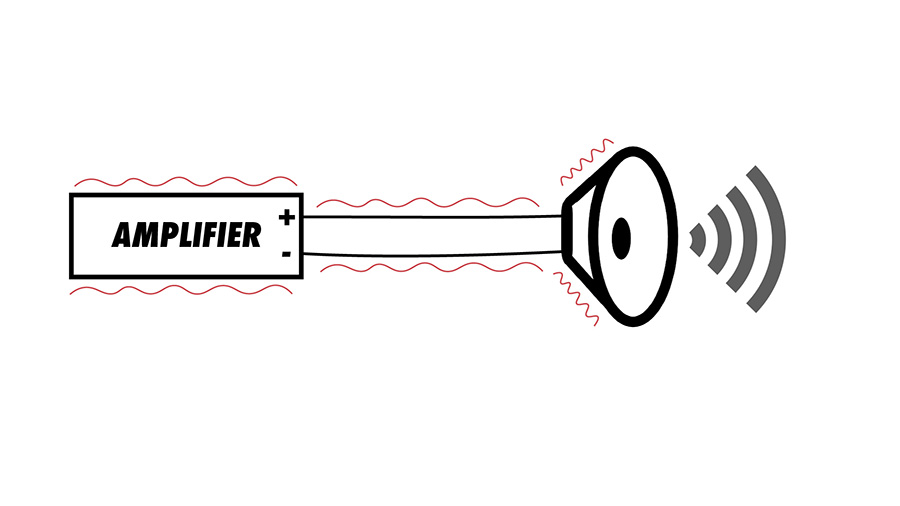
In this theoretical example, the speaker is an omnidirectional point source. That means the sound radiates equally in every direction from a single point in space. The sound moves further away from the speaker and it creates an expanding sphere of acoustic energy.
As the sphere grows larger, the acoustic energy created by the speaker is spread out over more and more surface area.
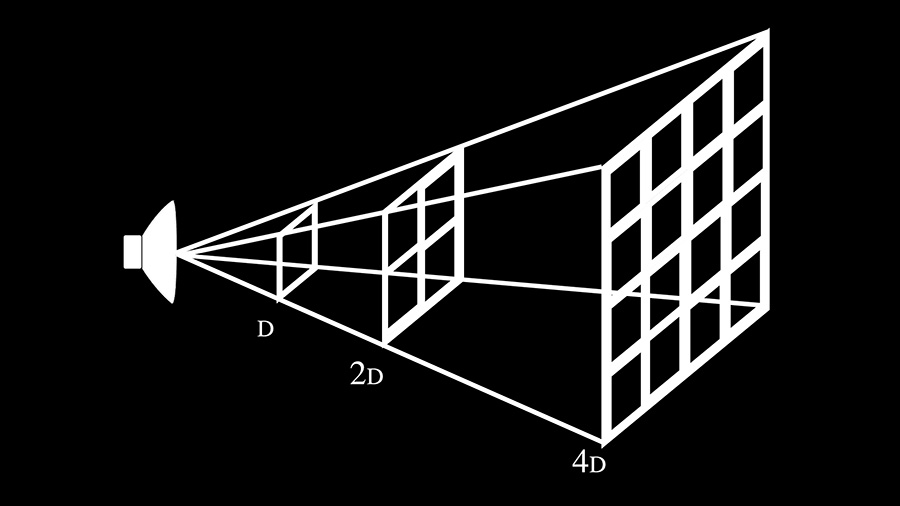
Naturally, the further the sphere of sound expands, the less energy there will be at any given section along its surface area. In other words, the sound intensity level (or energy per unit of surface area on that sphere) will decrease as the sound expands outward.
Understanding the intensity level is helpful, but we are usually most concerned with the sound pressure level at a given point in space, because that’s how our ears and microphones perceive sound.
From here on out, you will see “decibels” and “dB” used interchangeably. You may even see the term “dB SPL”, which means decibels sound pressure level. To learn more about decibels, you should check out this post: Decibels (dB): The Only 5 Things You (Probably) Need to Know
If two identical amplifiers provide 100 watts of power to two different speakers, one speaker may still be louder than the other depending on the sensitivity of each speaker.
The sensitivity of a speaker describes the sound pressure level that can be expected at a given power input. It’s typically shown as the sound pressure level at 1 meter away from the speaker with 1 watt provided by the amplifier.
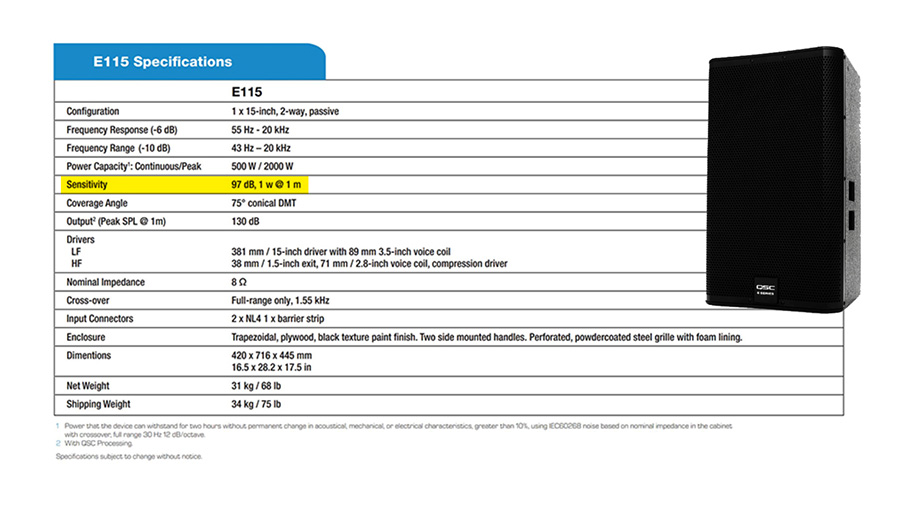
You can find the sensitivity of your speaker in the technical specifications online or in the user manual. For example, this QSC E115 speaker will produce 97 dB sound pressure level at 1 meter when provided with 1 watt of power.
So, if 1 watt of power will provide us with 97 dB at 1 meter, what sound pressure level can we expect with more power supplied from the amplifier? This question can be solved using the decibel formula below. I’ll do an example with the QSC E115, but you can plug in your own numbers.
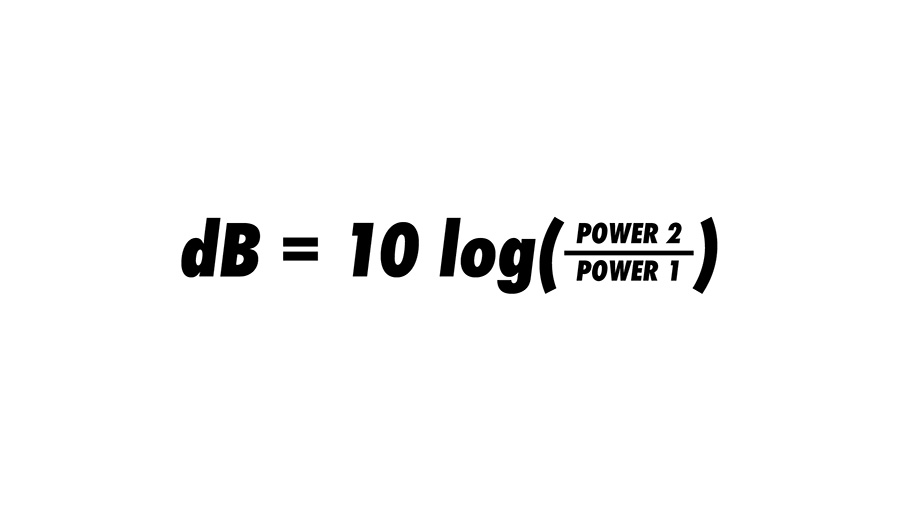
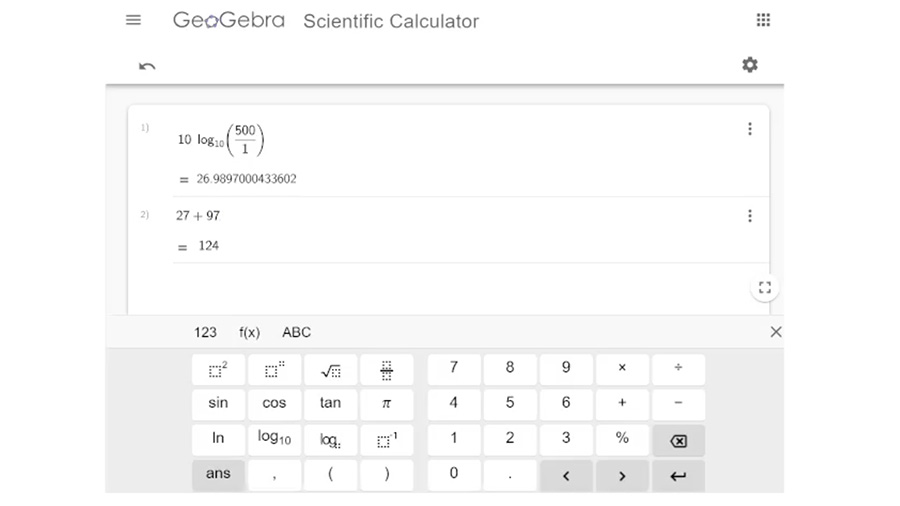
I’m going to find the continuous power capacity for this speaker, which is 500 watts. This means the speaker can remain stable with 500 watts of power supplied by the amplifier over an extended period of time. I’ll plug in 1 watt for the starting power, or power 1. Then I’ll plug in 500 watts for power 2. This formula will show the relationship between these two power values in decibels.
The ratio between 1 watt and 500 watts is about 27 dB. That means we will get 27 dB greater sound pressure level with 500 watts than we did with 1 watt. So we need to add 27 dB to the 97 dB speaker sensitivity spec, which shows that we can expect 124 dB with 500 watts at 1 meter from the speaker.
By the way, I want to offer you a free copy of my Speaker Specifications Guide that will help you understand the most important specs to look for when choosing a speaker.
Chances are, you won’t be listening to the speaker from 1 meter away. That means our next step is to figure out how much pressure level will be lost by the time the sound reaches the listening position.
The inverse distance law states that the sound pressure level is inverse to the distance from the sound source. In other words, each time we double the distance between the source and the listener, the sound pressure level decreases by 6dB.
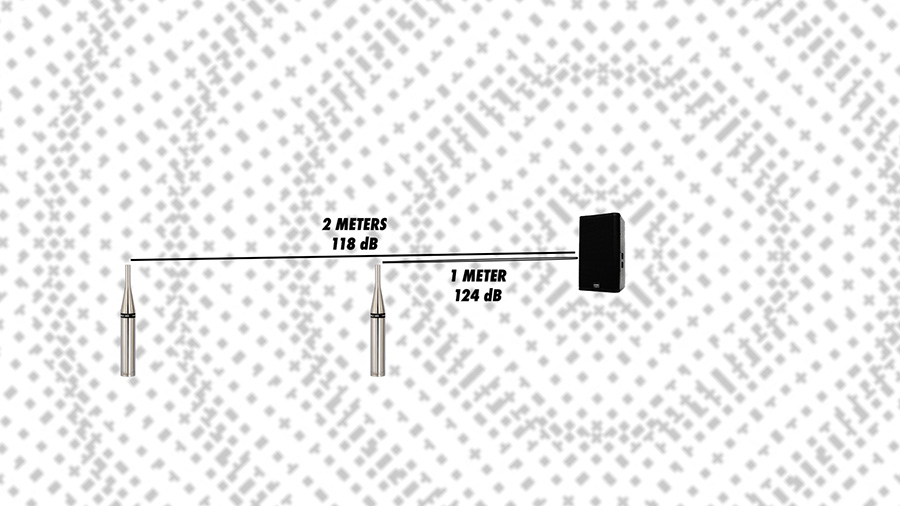
If we expect 124 dB sound pressure level from 500 watts at 1 meter away from the speaker, how much will we get at a listening distance of 2 meters? We doubled the distance, so we will get 6 dB lower sound pressure level, or 118 dB. This trick can be a useful tool for quick estimations. Each time you double the distance, subtract 6 dB.
However, if you know the listening distance, we can use a slightly different decibel formula and punch in the numbers. We use this formula because we are dealing with distance rather than the previous formula, which is used for comparing power.

This time, we will enter 1 meter (from the sensitivity spec) as distance 1 and 10 meters (the listening position) as distance 2. This calculator indicates that there will be a 20 dB loss over this distance, meaning that the 124 dB we calculated at 1 meter will be reduced to 104 dB at 10 meters.
There are a few more things you should consider when choosing your speakers… Watch this video to learn the 3 questions you should ask before buying.
