The decibel, or dB, is one of the most confusing concepts in audio production. Trying to wrap your mind around every detail of the decibel all at once is likely to leave you feeling overwhelmed.
The truth is: For most people, learning a few key principles about the decibel will be sufficient for working in the audio industry.
This article will provide you with everything you (probably) need to know about decibels.
1.) Decibels Can Represent Large Ratios With Simple Numbers
Decibels are used in several applications within the audio production industry. In this section, you’ll learn how the decibel simplifies calculations and communication in audio.
Making Sense of Large Numbers
The decibel compares two numbers that differ by many digits and represents the ratio of those numbers with a smaller, simpler number.
Decibels are especially useful when comparing numbers that vary by several orders of magnitude. That’s why the decibel is so commonly used to describe acoustical power, electrical power, and sound pressure level.
Decibels are logarithmic. They allow simple numbers to express values that would normally require many more digits.
For example, humans are capable of perceiving a vast range of sound pressure level, from subtle to extreme. When an absolute value is used to discuss sound pressure level, it becomes very challenging.
The pascal is a unit of measurement that describes air pressure in absolute terms of force per square meter. Humans are capable of hearing pressure changes from as subtle as 20 micropascals to as extreme as 20 pascals. The ratio between these values is 1:10,000,000!
It’s much easier to compare sound pressure levels when they are written in decibels, instead of pascals. This chart shows a side-by-side comparison of sound pressure levels presented as pascals and decibels:
| Sound Source | Sound Pressure (in Pascals) | Sound Pressure Level (in Decibels) |
|---|---|---|
| Threshold of Hearing (Quietest Sound) | 0.00002 Pa | 0 dB SPL |
| Normal Speech Level | 0.02 Pa | 60 dB SPL |
| Average Music Listening Level | 0.2 Pa | 80 dB SPL |
| Threshold of Pain (Extremely Loud) | 20 Pa | 120 dB SPL |
Human Perception of Hearing
The decibel is also useful because it presents changes in sound pressure on a scale that is more relevant to the way humans perceive loudness.
Most of us are accustomed to thinking in linear terms. For instance, twice the amount of letters produce a word twice as long. This mode of thinking doesn’t hold true for the way humans perceive the loudness of sound, however.
Thinking in linear terms, you might suspect that twice the amplifier power produces a sound twice as loud. This is not the case. The scale of human perception of loudness is closer to a logarithmic scale than a linear scale.
In a linear scale, each step is the same size, such as 10, 20, 30, 40 (each step is +10).
In a logarithmic scale, each step has the same proportion, such as 10, 100, 1000, 10000 (each step is *10).
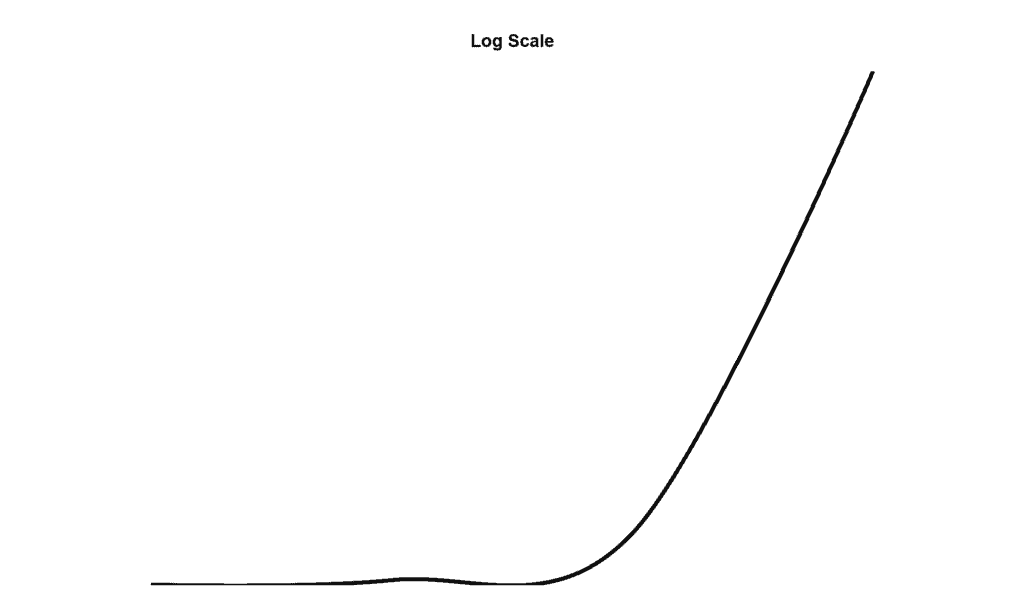
As sound pressure level increases, more and more power is required to produce the same perceived increase in loudness.
The decibel accounts for this phenomenon. Decibels present absolute values like the pascal or the watt on a logarithmic scale that is simpler to understand and better relates to the way we perceive changes in loudness.
The decibel tells us that the level difference caused by changing a value will depend on the initial value and the percentage that it has changed.
2.) Using Decibels Requires a Reference Point
A decibel is a way of describing the ratio between two quantities. When using decibels, you will always be comparing two values.
“The drums are 120 dB”, is an incomplete statement. That’s because the decibel, alone, has no value.
Decibels are only meaningful when describing the ratio between two quantities.
You could instead say, “the drums are 20 dB louder than the guitar”. This statement is more meaningful, because it draws a comparison between the level of the drums and the level of the guitar.
Decibels of Positive or Negative Change
Think of a fader on a mixing console. If the fader is placed at the 0 dB mark, or unity, it simply allows the audio signal to pass through. Pushing the fader above 0 dB will boost the signal. Pulling the fader below 0 dB will attenuate, or reduce, the signal.
In the case of a fader on a mixing console or in a DAW, unity gain is the 0 dB reference point. Decibel values above unity are positive and decibel values below unity are negative.
As you’ll see in the following section, each application of the decibel has its own 0 dB reference point. Values greater than that reference point are written as positive numbers, while values lesser than that reference point are written as negative numbers.
Common 0 dB Reference Points in Audio
Decibels can be used to describe quantities that relate to many things, including light, sound, radio waves, and electricity.
For many applications of the decibel, there are standardized reference points for defining 0 dB in absolute terms. Each application has its own suffix (i.e. dBm, dBu, dB SPL, etc.).
For the majority of audio professionals, it is most important to understand decibels as they relate to electrical power (dBm and dBW), electrical voltage (dBV and dBu), analog and digital audio meters (dBVU and dBFS), and sound pressure level (dB SPL).
Here is a helpful chart that defines the 0 dB reference point in common audio applications:
| Physical Unit | Abbreviation | 0 dB Reference |
|---|---|---|
| Voltage | dBV | 0 dB = 1 volt |
| Voltage | dBu | 0 dB = 0.775 |
| Electrical Power | dBW | 0 dB = 1 watt @ 50 ohms impedance (unless otherwise stated) |
| Electrical Power | dBm | 0 dB = 0.001 watts @ 600 ohms impedance |
| Sound Pressure | dB SPL | 0 dB = 0.00002 pascals (Human Threshold of Hearing) |
| Analog Audio Meter | dB VU (Volume Units) | 0 dB = +4 dBu (1.228 volts RMS) |
| Digital Audio Meter | dB FS (Full Scale) | 0 dB = Maximum Value in a Fixed Point System |
The references for 0 dB listed in this chart bring meaning to the various types of decibels. Let’s take a closer look at two of the most common applications in audio production: sound pressure level (SPL) and digital audio metering (dB FS):
Sound Pressure Level (dB SPL)
0 dB SPL, or sound pressure level, represents the Threshold of Hearing, or the quietest sound humans can hear. Therefore, we know that 80 dB SPL is 80 decibels louder than the quietest sound humans can hear.
Digital Audio Meter (dB FS)
0 dB FS, or full scale, refers to the maximum value in a fixed point digital system. Therefore, the highest level possible in a fixed point digital audio system is 0 dB FS.
If a digital audio signal exceeds 0 dB Full Scale in a fixed point system, digital clipping will occur. Digital audio levels are negative numbers (-12 dB FS, -20 dB FS, etc.). -12 dB FS is 12 decibels lower than the maximum level possible in a fixed point digital system.
3.) A Decibel is 1/10th of a Bel
In the following sections, you’ll learn how to make decibel calculations. This will allow you to find the ratio in decibels between absolute units like volts, watts, or pascals.
A decibel and a Bel have the same relationship as a decimeter and a meter. The formula for decibel calculations will make a lot more sense if you understand how the decibel relates to the Bel.
Calculating Ratios in Bels
The formula for finding the power ratio between two values in Bels is the following:
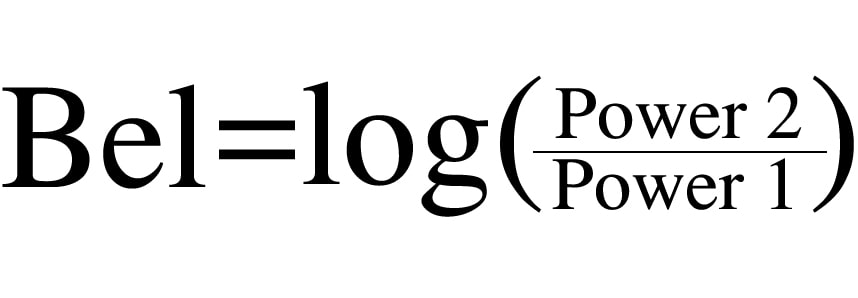
Power 1 is the reference power and Power 2 is the power being measured.
This formula can be solved using a calculator with the “log” function.
To do this, simply determine the ratio between the two powers by dividing the second power by the first power. Then find the log of that number by entering that number and pressing “log” on your calculator.
Let’s try this together. Say we want to find the ratio in Bels between 10 watts and 100 watts.
The formula would look like this:
Bel = log(100/10)
Dividing 100 by 10 gives us the ratio between them, which is 10.
Bel = log(10)
Using the log function of the calculator, we find that the log of 10 is 1.
Bel = 1
Therefore, the ratio between 10 watts and 100 watts is 1 Bel.
Calculating Ratios in Decibels
Now that you understand the basic formula used for calculating ratios in Bels, let’s see how we adjust that formula to calculate ratios in decibels.
The decibel is one tenth of a Bel. This is indicated by the metric prefix “deci-”.
This means we will need to multiply the Bel value by 10 to find the decibel value.
We now have the formula for decibel calculations:
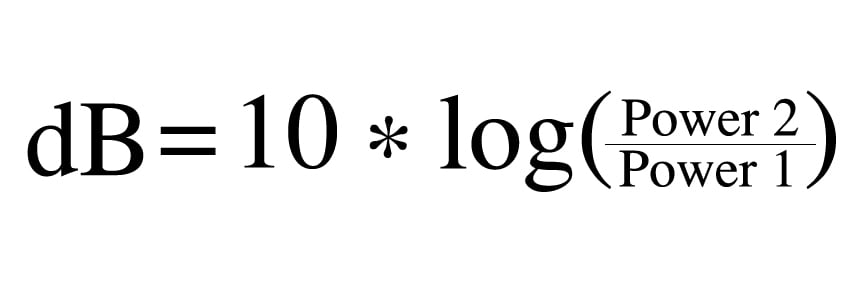
For comparison, let’s use the same power values as above (10 watts and 100 watts), this time finding the ratio in decibels.
dB = 10 * log(100/10)
Divide 100 by 10 to find the ratio, which is 10.
dB = 10 * log(10)
Use a calculator to find the log of 10, which is 1.
dB = 10 * 1
Multiply 1 by 10, which is 10.
dB = 10
Therefore, the ratio between 10 watts and 100 watts is 10 decibels, or 1 Bel.
Hopefully, you’re beginning to see that the decibel isn’t as confusing as it once seemed. To convert Bels to decibels, you simply multiply by 10.
4.) The Decibel Is a Power-Related Ratio
For many, the most confusing aspect of using the decibel is deciding which formula to use in a given situation.
The formula for decibels is the following:
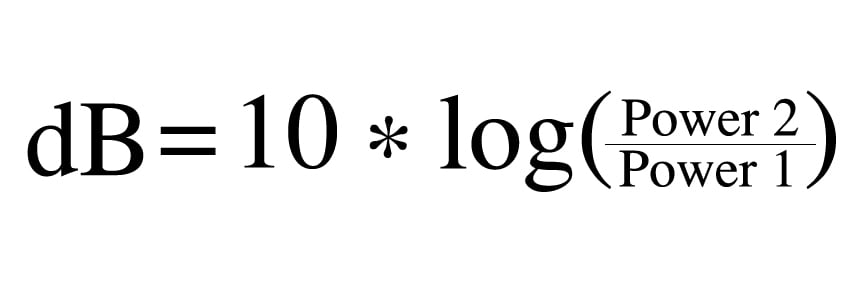
In some situations, however, this formula is used:
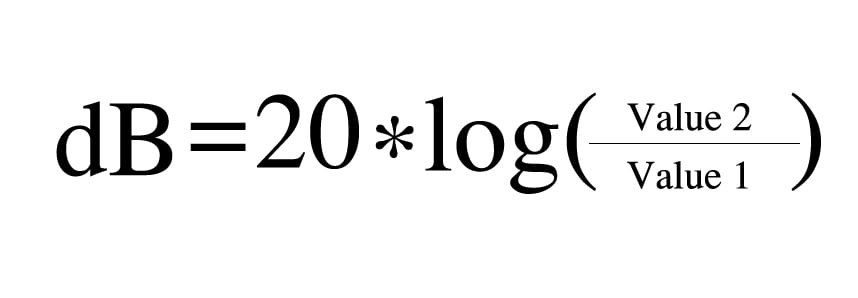
Why are different formulas used? How do you know which one is correct in a given situation? In this section, you’ll find out.
Calculating Power Ratios in Decibels
The decibel is always a power-related ratio.
When calculating electrical and acoustical power changes, use this formula:
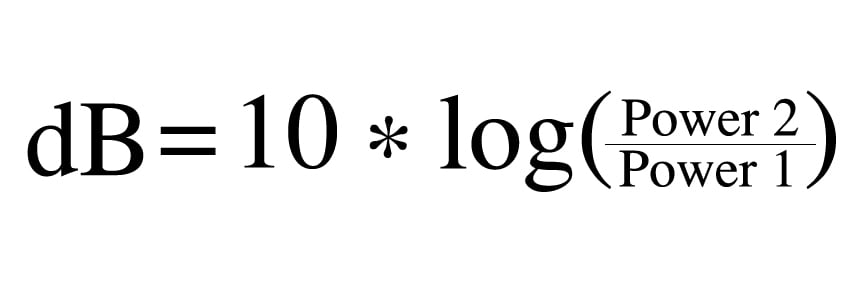
Calculating Non-Power Ratios in Decibels
The decibel can also be used to represent the ratio between non-power quantities.
When calculating voltage and acoustical pressure level changes, use this formula:
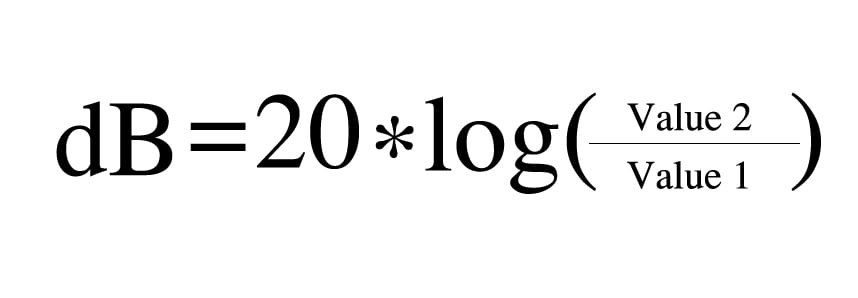
The reason we multiply by 20 is explained by the power equation, which is the following:
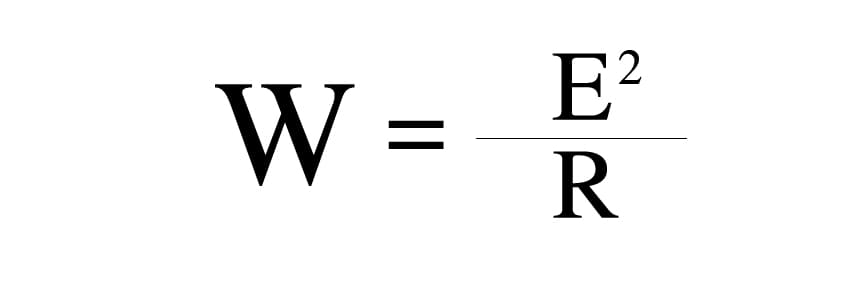
In this equation, W is power, E is voltage, and R is resistance.
Notice that voltage is squared. Power is proportional to voltage squared. This is why we multiply by 20 when finding decibels of voltage change.
Another way to come to the same answer would be to use the following formula:
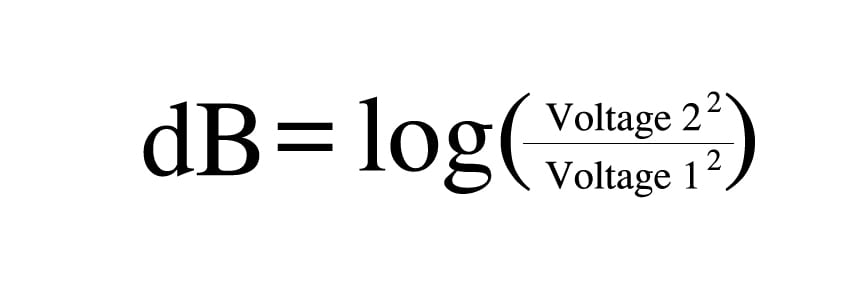
Quantities that are not powers must be made proportional to power.
As a recap, any time you are comparing power quantities in decibels, multiply the Bel formula by 10. Any time you are comparing non-power quantities in decibels, multiply the Bel formula by 20.
5.) 3 dB Indicates a Doubling of Power, 6 dB Indicates a Doubling of Voltage or Sound Pressure
It’s hard to get a straight answer when asking, “How many dB is a doubling?”. That’s because it depends on what is being doubled.
As you learned in the previous section, non-power quantities must be made proportional to power in order to be represented in decibels. This can be done by squaring each non-power quantity before finding the ratio between them, or by multiplying the Bel value by 20, instead of 10.
The decibel value to represent a doubling in power quantities is different from the value to represent a doubling in non-power quantities. In the context of audio production, voltage and sound pressure are the most common quantities that are not powers.
3 dB indicates a doubling of power, whereas 6 dB indicates a doubling of voltage or sound pressure level.
Benchmarks for Decibel Relationships
It is helpful to remember the decibel value for 2:1 and 10:1 changes of power, voltage, and sound pressure level. Use this chart for reference:
| Physical Unit | Ratio | dB Value |
|---|---|---|
| Power | 2:1 | 3 dB |
| Power | 10:1 | 10 dB |
| Voltage | 2:1 | 6 dB |
| Voltage | 10:1 | 20 dB |
| Sound Pressure Level | 2:1 | 6 dB |
| Sound Pressure Level | 10:1 | 20 dB |
Conclusion
I hope this has helped to clear up some of the confusion that surrounds decibels. Learning these key concepts will help open the door to becoming more comfortable with using decibels.
I believe it’s always worth the effort to understand something intuitively, rather than simply memorizing information. It may be helpful to revisit other explanations of the decibel you’ve encountered in the past, equipped with the information you learned in this article.
