For many, the definitions of the inverse square law that are found online are more confusing than they are helpful.
According to the Oxford Dictionary, the inverse square law states that “the intensity of [a sound wave] changes in inverse proportion to the square of the distance from the source.”
If you are seeking a simpler explanation, you’ve come to the right place. This article will help you to understand what the inverse square law means and how it relates to audio production.
The inverse square law states that with every doubling of distance away from the sound source, the sound will be four times less intense.
What is the Inverse Square Law?
In audio production, the inverse square law describes the reduction of a sound’s intensity over distance.
The inverse square law states that with every doubling of distance away from the sound source, the sound will be four times less intense.
If you’re unfamiliar with how sound travels through space, I recommend checking out a previous Audio University post called, Audio Basics: How Sound Works.
We all intuitively know that sounds get quieter as they travel further away from their sources. But, have you ever wondered why?
Intuitive Explanation of the Inverse Square Law
Perhaps you’re like me, finding the math more confusing than helpful. Let’s start by visualizing the math in action before learning the formulas that describe the inverse square law.
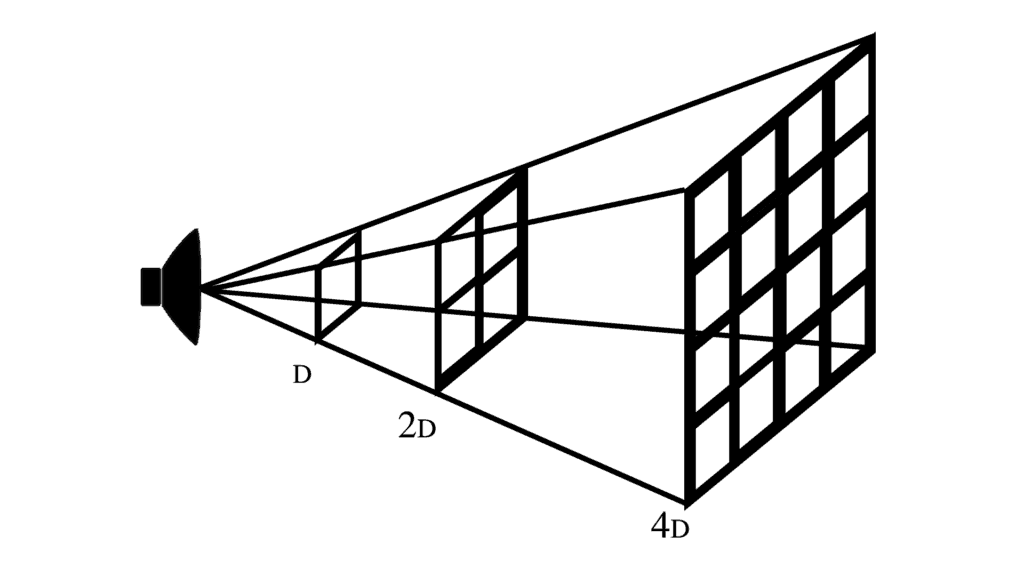
As a sound wave travels away from its source, a sphere of acoustical energy is formed. The finite amount of energy created by the sound source is spread thinner and thinner along the expanding surface area of the sphere..
In this image, the sphere on the left has a radius of 2 feet, while the sphere on the right has a radius of 4 feet. The sound source is located at the center of each sphere. So, think of the radius as the distance between you and the sound source.
While the radius of the second sphere is only twice the radius of the first sphere, the surface area of the second sphere is four times the surface area of the first sphere! Everytime the radius is doubled, the surface area is quadrupled.
The energy from the source is now spread out over four times the area, resulting in four times less energy per square meter.

Mathematical Explanation of the Inverse Square Law
If you do prefer to understand concepts using math, this section might be more helpful.
Step 1
To calculate the energy loss, we first need to know the area of the spherical wave front.
The formula used to find the area of a sphere is the following:
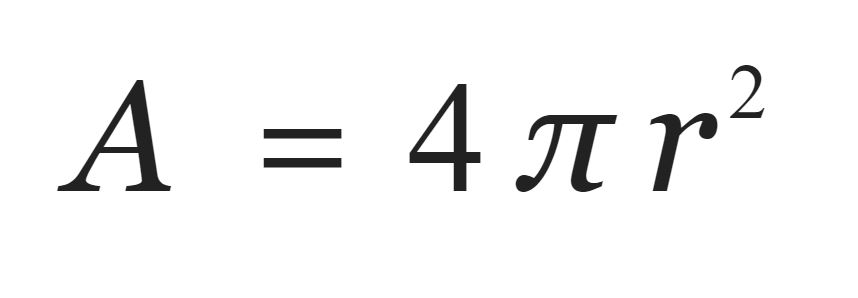
In this formula, r represents the radius of the sphere. In other words, r represents the distance from the sound source to the wave front.
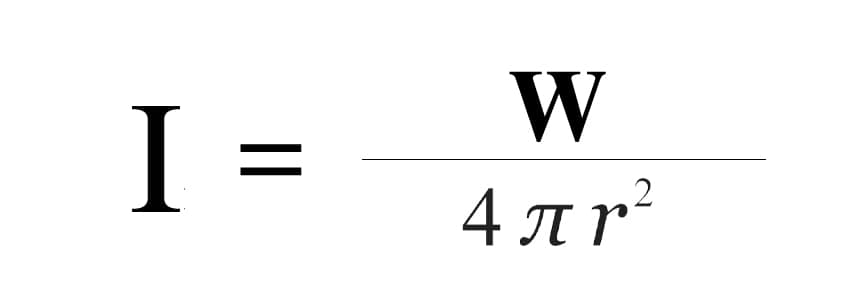
Thus, the intensity of a sound wave at a given distance from its source is proportional to the inverse square of that distance. Hence, the inverse square law.
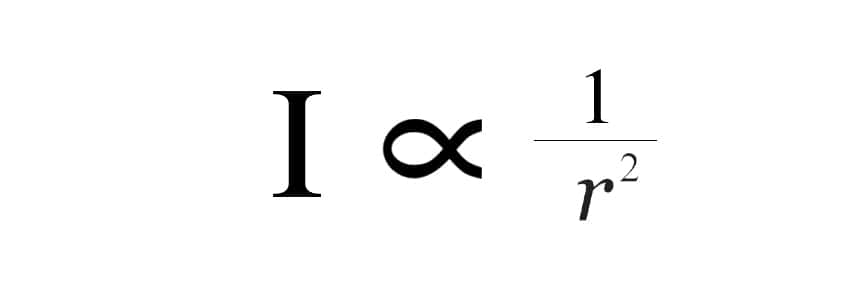
Calculating Sound Pressure Level Over Distance
The inverse square law helps us calculate the intensity level along the surface area of the wavefront.
However, our ears and microphones measure pressure level changes at only a small point along this surface area.
To measure pressure level changes at a given distance from a sound source, the inverse distance law is used. The inverse distance law states that sound pressure level at a given distance is proportional to the inverse of that distance.
Generally speaking, the inverse distance law is much more useful for audio production purposes.
Demonstration
A doubling of distance results in a 6 dB loss in both intensity (dB SIL) and pressure level (dB SPL).
In this video, you can see this demonstrated with a speaker and a microphone measuring sound pressure level from various distances.
Theory vs Reality: Inverse Square Law
While the inverse square law and the inverse distance law are powerful tools for solving real world problems, the simple relationships shown above assume theoretical conditions.
This section will explain the assumptions that prevent perfect calculations in real-world scenarios. Once you’re aware of these assumptions, you’ll be able to use the inverse square law and the inverse distance law without blindly trusting them in all situations.
Point Source
The first assumption is that the sound source is an omnidirectional point source.
This means that the sound source radiates sound in all directions evenly.
Free Field
The second assumption is a free field condition.
This means that there are no nearby obstructions or boundaries.
This is the most significant practical limitation. Rarely do we find situations without walls, floors, ceilings, or other barriers. A wall or other boundary could provide a reflection and thus cause less loss over distance than the inverse square law or inverse distance law would predict.
Conclusion
The inverse square law is a way of understanding something we already know on a basic level: that sounds get quieter as they travel away from their sources.
You can use it to predict sound intensity at a given distance from the sound source.
To predict sound pressure level, the inverse distance law is used.
Given that we do not live in a theoretical world, you must always take the assumptions of these laws into account.
